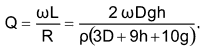Журнал РАДИОЛОЦМАН, январь 2012
В статье показано, как рассчитать индуктивность многослойной катушки без сердечника, зная только ее размеры и сопротивление постоянному току
Если размеры катушки выражены в миллиметрах, ее индуктивность в микрогенри может быть рассчитана по формуле:
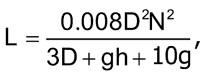
где
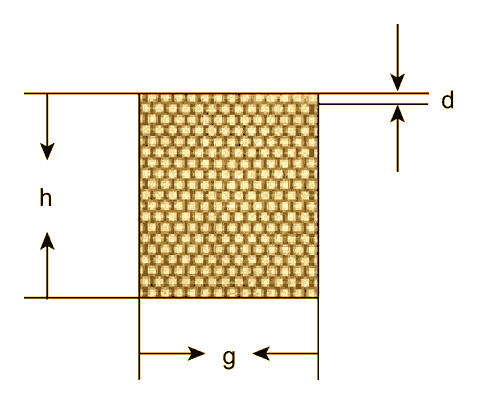
- D – средний диаметр катушки,
- h – высота катушки,
- g – глубина (толщина намотки) катушки,
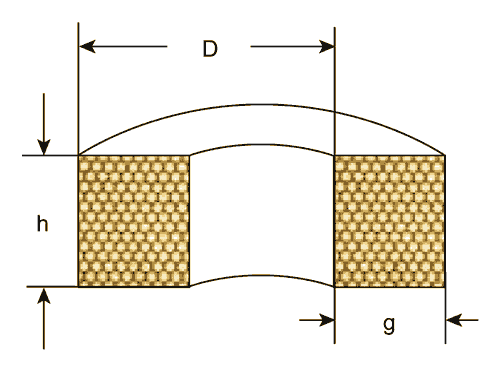
- N – количество витков (Рисунок 1).
 |
|
| Рисунок 1. | Зная размеры и количество витков катушки, можно рассчитать ее индуктивность. |
Если количество витков неизвестно, индуктивность, все равно, можно рассчитать, используя значение сопротивления обмотки постоянному току. Предполагается, что катушка намотана аккуратно, виток к витку, цилиндрическим эмалированным проводом (Рисунок 2). В этом случае приближенное выражение для числа витков будет следующим:
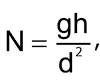
где d – диаметр провода.
Однако, мы будем полагать, что диаметр нам неизвестен.
 |
|
| Рисунок 2. | Оценить индуктивность аккуратно намотанной катушки можно по ее размерам и сопротивлению обмотки. |
Поскольку средняя длина витка равна π×D, общая длина провода будет N×π×D. Площадь сечения провода равна
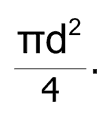
Сопротивление катушки R можно выразить как
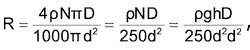
где ρ – удельное сопротивление, выраженное в [Ом·м], а сопротивление в [Ом]. Таким образом, можно получить выражение для квадрата диаметра провода:
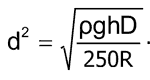
Теперь подставляем d2 в выражение для числа витков:
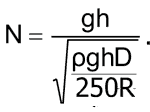
После возведения обеих частей уравнения в квадрат и сокращения дроби получаем
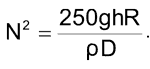
Подстановка N2 в первое уравнение дает

Подставив значение ρ для меди, получаем выражение для L, зависящее только от сопротивления и физических размеров катушки:
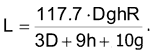
Попутно обратим внимание на интересный вывод, следующий из того факта, что R и L пропорциональны друг другу: добротность Q катушки с заданными размерами D, g и h при неизменной угловой частоте w =2πF является константой: