В статье предлагаются идеализированные частотно-зависимые однополюсные Pspice макромодели стандартного и полностью дифференциального операционного усилителя. Они достаточно точно описывают частотные и усилительные свойства большинства операционных усилителей этого типа. Применение этих моделей позволяет оценить верхнюю границу усиления и частоты единичного усиления операционного усилителя, который следует использовать в проектируемом усилительном или фильтрующем устройстве.
Введение
Одними их ведущих параметров операционного усилителя (ОУ) являются усиление с разомкнутой цепью обратной связи и частота единичного усиления [1, 2]. При разработке усилителей или активных фильтров на ОУ возникает проблема выбора конкретного типа ОУ, для реализации заданных технических характеристик. Выбор ОУ с завышенными характеристиками может привести к удорожанию устройства. Поэтому возникает потребность в простой частотно-зависимой однополюсной Pspice модели ОУ, которая позволит оценить верхнюю частотную и усилительную границу ОУ, при которой усилитель или активный фильтр обеспечит требуемые частные характеристики. Т.е. если выбрать ОУ не хуже, то устройство должно работать.
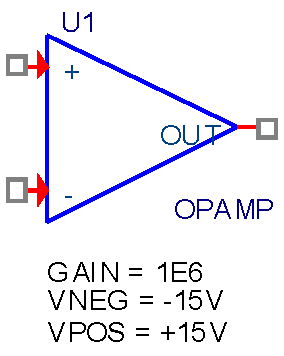
В OrCAD v16.6 [3, 4, 5] есть простая модель идеализированного частотно-независимого операционного усилителя OPAMP (Рисунок 1). Она находится в библиотеке analog.olb. Усиление ОУ по умолчанию GAIN=1MEG. Напряжения питания ОУ по умолчанию VPOS=+15V, VNEG=-15V. Работа модели OPAMP описывается шаблоном PSpice Template (Рисунок 1), в котором записано математическое выражение на языке PSpice, использующее функцию LIMIT. Функция LIMIT требуется, чтобы ограничить выходное напряжение этой модели ОУ в диапазоне напряжений питания реального ОУ (VNEG, VPOS). Стандартное питание ОУ ±15 В.
Таким образом, задача сводится к тому, чтобы создать модель такими же характеристиками по постоянному току, но с добавлением одного частотного полюса.
 |
|
| Рисунок 1. | УГО идеализированного стандартного ОУ из библиотеки analog.olb и его PSpice Template (шаблон) |
PSpice Template = E^@REFDES %OUT 0 VALUE {LIMIT(V(%+,%-)*@GAIN,@VNEG,@VPOS)}
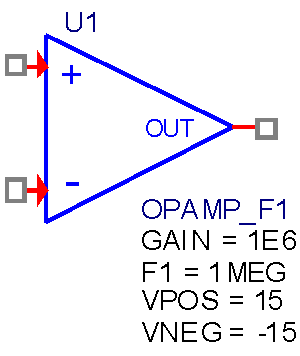
УГО частотно-зависимой макромодели стандартного ОУ, получившей имя OPAMP_F1, показано на Рисунке 2. Как видим, его УГО они ничем не отличаются от модели обычного ОУ с именем OPAMP, но среди параметров, модели ОУ которые можно изменять, появился параметр F1 – частота единичного усиления.
 |
|
| Рисунок 2. | УГО идеализированной частотно-зависимой макромодели стандартного ОУ |
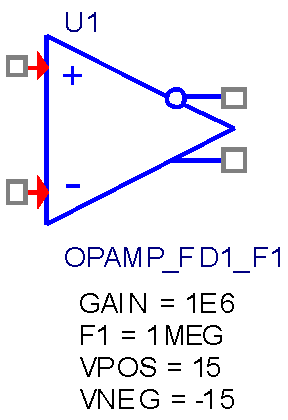
УГО частотно-зависимой макромодели полностью дифференциального ОУ без входа смещения, получившей имя OPAMP_FD1_F1, показано на Рисунке 3.
 |
|
| Рисунок 3. | УГО идеализированной частотно-зависимой макромодели полностью дифференциального ОУ без входа смещения |
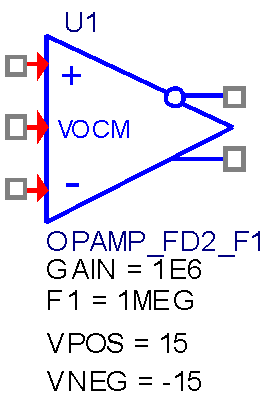
УГО частотно-зависимой макромодели полностью дифференциального ОУ c входом смещения VOCM, получившей имя OPAMP_FD2_F1, показано на Рисунке 4.
 |
|
| Рисунок 4. | УГО идеализированной частотно-зависимой макромодели полностью дифференциального ОУ c входом смещения VOCM |
Среди параметров полностью дифференциальных ОУ, которые можно изменять, имеется параметр F1 – частота единичного усиления.
Математическая модель стандартного ОУ с одним частотным полюсом
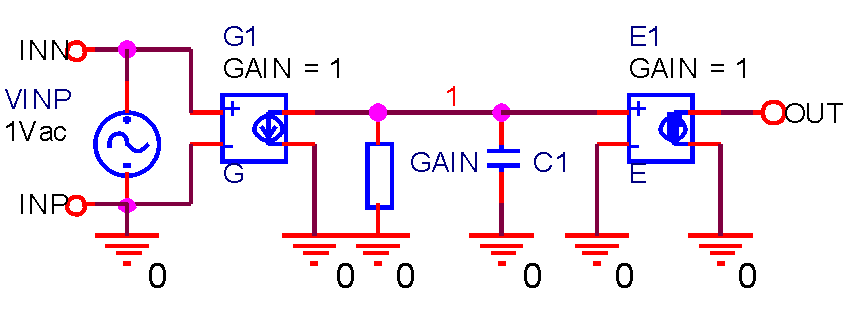
На Рисунке 5 изображена линеаризированная схема частотно-зависимой однополюсной макромодели стандартного ОУ. Она состоит из источника тока управляемого напряжением (ИТУН) G1 с единичным усилением, нагруженного на параллельно соединённые резистор с именем GAIN и конденсатор С1. Напряжение узла 1, буферизировано источником напряжения управляемого напряжением (ИНУН) E1 с единичным усилением. Усиление по напряжению в этой схеме достигается за счёт протекания тока от ИТУН G1 через резистор GAIN.
 |
|
| Рисунок 5. | Схема линеаризированной частотно-зависимой однополюсной макромодели стандартного ОУ |
Листинг 1
Составим систему уравнений Кирхгофа для схемы (Рисунок 5).
> restart:
> -VINP-V1*s*C1-V1/GAIN=0; VOUT=V1;
*****************************************************************************************
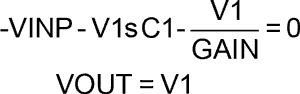
Решим эту систему уравнений относительно V1, VOUT и найдём операторную передаточную функцию ОУ с разомкнутой ОС.
> solve({%%,%},{V1,VOUT}): assign(%):
W:=VOUT/VINP;
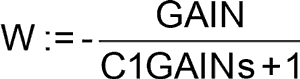
Переведём передаточную функцию в частотную область.
> K:=subs(s=I*2*Pi*f,W);
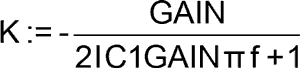
Составим и решим уравнение, из которого найдём частоту F1, на которой модуль передаточной функции в частотной области равен 1.
> F1=solve(evalc(abs(K))=1,f)[1];

Считая GAIN заданным, выразим C1 через частоту единичного усиления через F1.
> C1:=solve(%,C1);

Запишем это выражение в формате Pspice для последующего использования в макромоделях.
| C={SQRT(GAIN^2-1)/2/F1/Pi/GAIN} | (1) |
Создание макромоделей ОУ
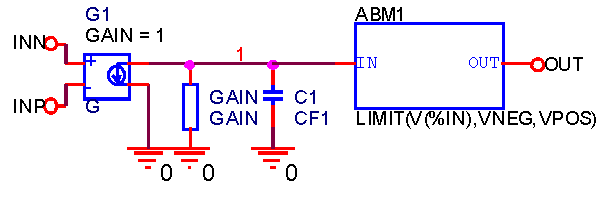
Для начала построим поведенческую модель частотно-зависимой макромодели стандартного ОУ (Рисунок 6). Для этого будем использовать блоки поведенческого моделирования из библиотеки ANALOG.olb и AMB.olb [3, 6]. Поведенческий блок AVM1, по аналогии с моделью OPAMP (Рисунок 1), на языке Pspice описываются выражением LIMIT( V(%IN) , VNEG, VPOS).
 |
|
| Рисунок 6. | Поведенческая модель частотно-зависимого стандартного ОУ. |
Схема нарисована таким образом, что было удобно сделать экстракцию Pspice макромодели частотно-зависимого ОУ. Для экстракции заготовки макромодели требуется сгенерировать NET-листинг (Листинг 2) в OrCAD Capture (Даже если транслятор в Pspice NET-листинг выдаст сообщение об ошибке надо продолжить трансляцию NET-листинга, она все равно состоится). Эту заготовку надо оформить в макромодель по правилам Pspice и создать условное графическое изображение, чтобы использовать её в схемных проектах. Готовая Pspice макромодель частотно-зависимого ОУ для OrCAD v16.6 представлена в Листинге 3, а для OrCAD v9.1 в Листинге 4. Макромодель получила имя OPAMP_F1. Для OrCAD v9.1 макромодель будет немного отличаться, так как число Pi требуется указать явно директивой .PARAM.
Глядя на текст макромодели (Листинг 3, 4) видим, что за усиление GAIN отвечает резистор R_GAIN, а за частоту единичного усиления F1 отвечает модель конденсатора с именем CF1. Параметр С модели CF1 записан формулой, в соответствии с (1). При запуске моделирования PSpice вычислит требуемую ёмкость по этой формуле, исходя из заданных параметров GAIN и F1, и подставит её как номинал С1.
Листинг 2
* source ORCAD_166
C_C1 0 1 CF1 TC=0,0
R_GAIN 0 1 GAIN TC=0,0
G_G1 1 0 INN INP 1
E_ABM1 OUT 0 VALUE { LIMIT(V(1),VNEG,VPOS) }
Листинг 3
* PSpice Model Editor - Version 16.6
*$
* Device type: Frequency-dependent standard operational amplifiers
* Device name: OPAMP_F1
* Aythor: Petrakov Oleg [email protected]
* Date: 25 August 2016
*
* F1 - Freguence single gain
* GAIN - Gain with the opened feedback coupling
*
.subckt OPAMP_F1 INP INN OUT
+ PARAMS: GAIN=1e6 F1=1MEG VPOS=15 VNEG=-15
C1 0 1 CF1 1
R_GAIN 0 1 {GAIN}
G1 1 0 INN INP 1
E1 OUT 0 VALUE {LIMIT(V(1),VNEG,VPOS)}
.model CF1 CAP C={SQRT(GAIN^2-1)/2/F1/Pi/GAIN}
.ends
*$
Листинг 4
* PSpice Model Editor - Version 9.1
*$
* Device type: Frequency-dependent standard operational amplifiers
* Device name: OPAMP_F1
* Aythor: Petrakov Oleg [email protected]
* Date: 25 August 2016
*
* F1 - Freguence single gain
* GAIN - Gain with the opened feedback coupling
*
.subckt OPAMP_F1 INP INN OUT
+ PARAMS: GAIN=1e6 F1=1MEG VPOS=15 VNEG=-15
.PARAM: Pi=3.1415926535897932385
C1 0 1 CF1 1
R_GAIN 0 1 {GAIN}
G1 1 0 INN INP 1
E1 OUT 0 VALUE {LIMIT(V(1),VNEG,VPOS)}
.model CF1 CAP C={SQRT(GAIN^2-1)/2/F1/Pi/GAIN}
.ends
*$



